Les adaptations en mathématiques

En scolaire, on distingue adaptations et modifications dans les plans d'intervention (PI). Tout enseignant connaît bien la différence, mais si vous êtes un parent ou un professionnel hors système scolaire, cette distinction n'est possiblement pas si claire pour vous.

Adaptation : mesure qui n’affecte pas les exigences liées aux tâches ni le contenu d’apprentissage ou les critères d’évaluation.

Modification : mesure qui diminue le niveau de difficulté ou les exigences de réalisation des tâches.

Ces mesures cherchent à répondre aux besoins spécifiques de l'élève, identifiés dans la démarche de son PI. Un exemple de mesure d'adaptation fréquemment mise en place est le temps supplémentaire. L'élève qui en bénéficie aura droit, par exemple, au tiers du temps prévu pour une évaluation en plus du temps alloué à tous. Autrement dit, pour une évaluation d'une heure, cet élève aura droit à 1h20. Une telle mesure cadre bien évidemment dans l'adaptation et non dans la modification.

La mise en place de modifications fait suite à une démarche sérieuse durant laquelle les mesures d'adaptation employées n'ont malheureusement pas suffi pour assurer la réussite académique. Rendu à cette étape, le bulletin inclut des notes modifiées, du moins pour les matières concernées par ces mesures. En effet, ces notes ne sont plus comparables à celles des autres élèves de la classe, puisque les critères d'évaluation sont modifiés.

Dans ce billet, j'engage une réflexion sur les mesures d'adaptation. Pour ce faire, je tracerai quelques parallèles entre les mesures communément acceptées pour les élèves ayant des besoins en écriture et pour ceux ayant des besoins en mathématiques.

Le prédicteur de mots orthographique

Les mesures d'adaptation pour les élèves ayant des besoins en lecture ou en écriture sont plutôt nombreuses. Les plus connues sont certainement le prédicteur de mots (une fonction d'aide de logiciels tels que WordQ ou Lexibar) et la synthèse vocale (autre fonction d'aide fournie par ces mêmes logiciels). Je me pencherai un peu plus en détail sur le prédicteur de mots orthographique.

Cette fonction d'aide consiste à fournir à l'élève une liste de mots bien orthographiés dont les premières lettres correspondent à celles que l'élève a tapées. Par exemple, après avoir tapé "car", WordQ me propose cette liste de mots :

1. car

2. carte

3. caractère

4. carrière

5. cartes

Advenant que je souhaite en fait écrire le mot "cartable", il me faudra poursuivre mon encodage. C'est finalement rendu à "carta" que WordQ me propose pour la première fois le mot cartable, et ce, au numéro 1. J'ai alors le choix de taper sur le "1" de mon clavier ou de cliquer directement sur le mot dans la boîte de mots. Ainsi, le prédicteur complétera le mot à mon écran, sans que j'aie à entrer moi-même les lettres "ble". Pour un tel mot régulier, c'est-à-dire respectant les régularités orthographiques, le prédicteur de mots ne semble pas être d'une si grande aide. Par contre, face à un mot inconsistant, comme "descendre", l'élève dont le lexique orthographique* est peu développé pourra certainement éviter une erreur orthographique en testant quelques hypothèses, et ce, jusqu'à ce que WordQ lui propose finalement le bon mot.

*Lexique orthographique : ensemble des mots, sous leur forme écrite (ex. "éléphant"), connus par un élève. C'est en quelque sorte son dictionnaire mental.

Je rappelle que cette fonction d'aide est une adaptation. Il est donc officiellement considéré que celle-ci ne diminue pas le niveau de difficulté ou les exigences de la tâche d'écriture. Toutefois, elle compense pour l'élève ayant consolidé peu de représentations orthographiques*, comparativement à ses pairs.

*Représentation orthographique : c'est la forme écrite d'un mot. Par exemple, "éléphant" est une représentation orthographique.

Le prédicteur de mots pallie une difficulté spécifique qui fait en sorte qu'un élève a besoin de plus d'expositions et d'un apprentissage encore plus explicite que ses pairs pour consolider des représentations orthographiques en mémoire à long terme. Cet élève construit donc évidemment son lexique orthographique à vitesse réduite. Son lexique phonologique* et son lexique orthographique présentent un écart de taille significativement plus important que ses camarades de classe.

*Lexique phonologique : ensemble des mots, sous leur forme orale (ex. /elefã/), connus par un élève.

Le prédicteur de mots s'avère alors une mesure d'adaptation nécessaire, afin que cet élève ne réduise pas la complexité du langage qu'il souhaite utiliser en écriture, évitant les mots dont il ignore l'orthographe.

La table de Pythagore

Eh bien, l'élève qui présente des difficultés en mathématiques présente parfois (souvent) une faiblesse similaire. Effectivement, il arrive fréquemment que des élèves aient des difficultés marquées à apprendre "par cœur" leurs tables de multiplication. Cette difficulté engendre de nombreuses conséquences. Si des stratégies de comptage efficientes permettent de calculer sommes et différences avec relativement peu d'efforts, l'usage de stratégies mentales de comptage (par bonds) ou de décomposition (ex.: 4 x 3 = 4 x 2 + 4 x 1 = 8 + 4 = 12) s'avère beaucoup plus épuisant et taxe considérablement les ressources très limitées de la mémoire de travail.

Je serais bien curieuse de connaître le nombre de faits de multiplication et de division* qu'un élève doit récupérer en moyenne dans le cadre d'une évaluation de compétence 2, au 3e cycle du primaire.

*Faits de multiplication ou faits multiplicatifs : association en mémoire à long terme entre deux facteurs à un chiffre et leur produit (ex.: 8 x 7 = 56).

*Faits de la division : association en mémoire à long terme entre un dividende, un diviseur à un chiffre et un quotient à un chiffre (ex.: 56 ÷ 8 = 7).

Ces faits ne sont pas requis uniquement pour les calculs multichiffres tels que 325 x 56. Ils sont également essentiels lors du traitement des fractions (pour les simplifier, pour les additionner, etc.), dans le cadre de l'apprentissage de diverses compétences numériques (ex. : la factorisation, la priorité des opérations, le plus petit commun diviseur, la probabilité, etc.) et leur connaissance sera déterminante quand viendra le temps d'aborder l'algèbre.

L'élève avec des difficultés en orthographe lexicale

Lorsque la récupération en mémoire à long terme d'une représentation orthographique échoue, l'élève sans mesures d'adaptation a quelques options :

• Il peut encoder le mot en le segmentant en phonèmes, en appliquant les correspondances phonèmes-graphèmes (CPG) (ex.: le son /wɛ̃/ s'écrit "oin") et en respectant les régularités orthographiques (ex. : le son /ɛ̃/ s'écrit généralement "in"). Cette option mènera parfois / souvent à l'erreur :

  • parce que l'élève ne maîtrise pas la segmentation phonémique et les CPG (ex. : il écrit "fouin" pour "foin")

  • parce qu'il ne connaît pas (toutes) les régularités orthographiques (ex. : il écrit "lapain" pour "lapin")

  • parce que certains mots sont inconsistants et qu'il est donc impossible de les écrire correctement lorsqu'on n'a pas consolidé la représentation orthographique (ex. : il écrit "mecieu" pour "monsieur")

  • et parce que d'autres, sans être inconsistants, nous laissent dans le doute (ex.: prendre ou prandre ?).

• Il peut consulter un outil disponible pour l'ensemble des élèves (ex. : un dictionnaire). Cette option mène plus assurément au succès. Toujours faut-il, toutefois, savoir utiliser efficacement l'outil en question et avoir suffisamment de temps pour effectuer plusieurs recherches.

Effectivement, écrire des mots dont on ignore l'orthographe, ça prend du temps. Quand on doit le faire pour une grande proportion des mots qu'on souhaite écrire, ça décourage.

Le prédicteur de mots est donc une mesure qui répond au besoin de l'élève. Grâce à cette mesure, l'élève ne sera pas épuisé par la tâche d'écriture. On pourra voir son plein potentiel dans ses autres compétences de base (notamment, les erreurs grammaticales seront probablement moins nombreuses, car les ressources cognitives ne sont pas toutes allouées à l'orthographe lexicale) et dans ses compétences de haut niveau, c'est-à-dire en production de texte (les phrases de l'élève reflètent alors davantage son niveau de langage : des constructions syntaxiques plus complexes et diversifiées, un lexique plus riche, etc.).

L'élève avec des difficultés avec les faits multiplicatifs

Lorsque la récupération en mémoire à long terme d'un fait multiplicatif échoue (ex. : 4 x 3 = ???), l'élève sans mesures d'adaptation a quelques options :

• Il peut représenter les quantités (avec du matériel ou en dessinant) et dénombrer pour composer le nombre recherché (le produit)

  

• Il peut compter par bonds (ex.: 3, 6, 9, 12)

• Il peut faire une addition répétée (ex. : 3+3 =6; 6+3=9; 9+3=12)

• Il peut décomposer un des facteurs et utiliser la propriété de la distributivité de la multiplication (ex. : 3 x (2 + 2) = (3 x 2) + (3 x 2) = 6 + 6 = 12)

Contrairement à l'élève présentant des difficultés en orthographe lexicale, celui-ci n'a pas accès à un outil disponible pour l'ensemble des élèves qui lui permettrait à coup sûr de valider sa réponse. En effet, lors des évaluations en mathématiques au primaire, il est exceptionnel que les élèves puissent utiliser la calculatrice ou consulter une table de Pythagore. Notez bien que ce n'est pas interdit formellement et qu'un enseignant pourrait choisir de permettre leur usage à l'ensemble de la classe, à sa discrétion (sauf pour certaines évaluations ministérielles de 6e année). Quoi qu'il en soit, au primaire, ce choix n'est pas traditionnel.

Or, les options qui s'offrent à l'élève ne garantissent pas la réussite. L'élève est sujet à la surcharge cognitive, ce qui augmente les chances d'erreurs. Si vous n'avez jamais visionné cette capsule vidéo, elle illustre bien ce phénomène.

Quelle adaptation offrons-nous donc, en scolaire, pour contrer cette difficulté, pour éviter que l'élève ne s'épuise et ne commette des erreurs consécutives à son état de surcharge cognitive ? La réponse est que généralement, on ne fournit aucune adaptation, sauf pour la compétence 1 (résoudre) pour laquelle l'élève peut avoir droit à la calculatrice. Pour être tout à fait honnête, lors des évaluations de la compétence 2 (raisonner), on prévoit parfois une adaptation : une table de Pythagore... vide ! Ce qui n'est pas dans la mémoire à long terme (les produits) n'est pas non plus dans cette table vide.

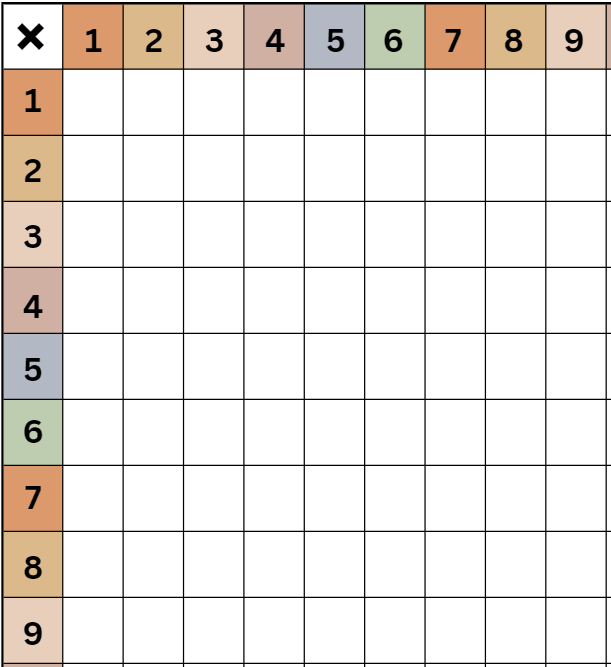
Mais à quoi ça sert alors ? On nous dira que l'élève pourra apprendre à inscrire tout calcul réalisé au cours de son évaluation dans la table et donc, si ce même calcul doit être réalisé une seconde fois, il n'aura pas à refaire ce même calcul. Il pourrait aussi prendre le temps de remplir la table au complet en début d'évaluation (en comptant par bonds ou en faisant des additions répétées, par exemple). Si une erreur se glisse dans la table (ex. : car l'élève commet une erreur dans ses bonds), elle sera reproduite chaque fois que l'élève reprendra sa donnée erronée dans sa table.

Nos voisins les Américains

Aux États-Unis, chaque état détermine quelles adaptations sont permises, tout comme au Canada, chaque province se positionne à cet égard. Je me suis questionnée si la table de Pythagore (une vraie de vraie table complète) était permise autre part, comme mesure d'adaptation (et non de modification). Il s'avère que nos voisins américains la permettent en majorité. En effet, 33 états considèrent la table de Pythagore comme une adaptation (Designated features et Accomodations sont deux formes d'adaptations) et 2 états la permettent même en tout temps à l'ensemble des élèves (voir figure ci-dessous, tirée de https://publications.ici.umn.edu/nceo/accommodations-toolkit/math-charts-tables-policies) :

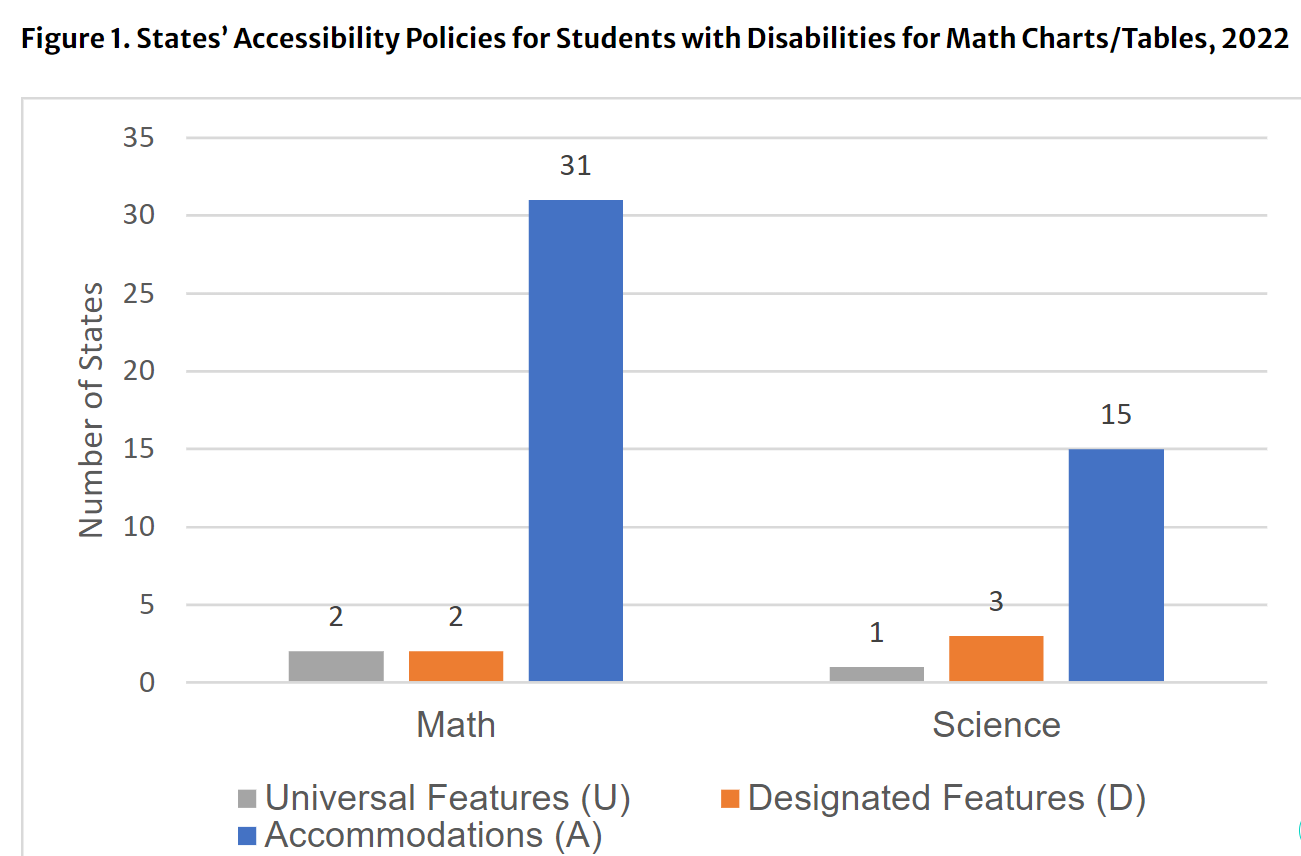
Les élèves présentant des difficultés en mathématiques ont peu d'allègements dans notre système scolaire québécois. Cette restriction n'est à mon avis pas justifiée. Sauf lors d'une évaluation formative de type "math chrono" qui évalue directement les faits multiplicatifs, l'accès à une table de Pythagore ne diminue pas le niveau de difficulté ni les exigences de réalisation des tâches.

L'autre côté de la médaille

Je dois avouer qu'il y a bien un risque potentiel à l'octroi d'une table de Pythagore. Il ne faudrait que l'élève cesse ses efforts pour apprendre les tables de multiplication sous prétexte qu'il a maintenant accès à une telle adaptation. Pareillement, les adultes qui l'entourent doivent poursuivre le travail en ce sens, encourager l'élève, le guider vers l'atteinte de la fluence arithmétique*.

*Fluence arithmétique : capacité de résoudre correctement et rapidement (sans effort) des problèmes arithmétiques simples (ex. : 3 + 8 ; 12 - 7 ; 5 x 6 ; 49 ÷ 7)

En effet, la fluence des faits multiplicatifs est un prédicteur unique des habiletés procédurales sur les fractions et est corrélée à un meilleur traitement des fractions (Hansen et al., 2015; Wortha et al., 2023). Il faut savoir que l'élève ayant accès à une table de Pythagore complète est encore désavantagé par rapport aux élèves qui ont réussi à consolider leurs tables de multiplication. Le fait de devoir recourir à un outil externe ralentit, on perd parfois notre place dans un algorithme complexe. L'effet de l'attention partagée de la théorie de la charge cognitive suggère d'ailleurs que le recours à un outil externe engendre une charge cognitive plus importante. De plus, les relations entre les nombres doivent être recherchées dans une table, elles ne nous sautent pas aux yeux, comme lorsqu'on connaît nos tables. Pour illustrer cette situation, je vous invite à simplifier la fraction 12/27. Si vous connaissez vos tables, vous aurez très rapidement identifié un diviseur commun : le 3. La simplification est ensuite réalisée en toute simplicité : 4/9. Bingo ! Si la table de Pythagore peut servir à cette fin, l'élève devra certes avoir été entraîné auparavant à cet usage alternatif (ici, la première étape de l'élève ne consiste pas à trouver le produit de deux facteurs en identifiant la bonne rangée et la bonne colonne de la table à double entrées) et même alors, le repérage des deux nombres sur une même ligne ou colonne prendra plus de temps que ce dont vous avez eu besoin pour identifier mentalement le diviseur commun.

La table de Pythagore est un support dont l'usage devrait être temporaire. Contrairement au lexique orthographique, les tables de multiplication sont en quantité limitée. En effet, si l'on exclut la table du 0 et celle du 1, qui ne nécessitent pas un apprentissage par cœur, et en considérant la compréhension de la commutativité, ce sont uniquement 36 faits multiplicatifs qu'un élève doit apprendre. Et bien évidemment, ces faits permettent aussi de résoudre les faits de la division, car l'élève doit comprendre qu'il s'agit d'opérations inverses. Cet apprentissage est à la portée de tous si l'on met en place des activités efficaces et un dosage suffisant.

Dans mon monde idéal

Alors ici, je me permets de rêver un peu. Dans mon monde idéal, l'élève repéré par son enseignant comme présentant des difficultés significatives avec l'apprentissage des tables de multiplication aurait droit à des interventions en sous-groupe (palier 2). Dans une même école, il ne serait certainement pas difficile d'identifier une poignée d'élèves pouvant bénéficier d'un tel traitement. Ces élèves auraient 5 à 10 minutes par jour allouées à l'apprentissage des faits multiplicatifs. Parce que l'atteinte de l'objectif ultime, même sous ces excellentes conditions, prendra certainement plusieurs semaines, voire plusieurs mois, l'élève aurait droit, conformément à ce qui serait inscrit dans son PI, à une table de Pythagore complète ou partiellement complétée. Le principe serait le suivant : lorsqu'une table atteindrait les critères de maîtrise (précision et fluence)*, cette table disparaîtrait de la table de Pythagore de l'élève. Petit à petit, la table serait de moins en moins remplie et éventuellement, ce support n'aurait plus d'utilité.

*Pour approfondir la notion de fluence arithmétique, voir : https://genevieverainville.podia.com/dcpm-une-donnee-essentielle-de-fluence-arithmetique

Cette diminution progressive du support est primordiale pour que les tables travaillées se consolident vraiment. En effet, la pratique de récupération joue un rôle clé dans l'apprentissage à long terme. Lorsque l'élève consulte une table de Pythagore partiellement complétée et qu'il constate que le produit recherché n'y est pas, il n'a d'autre choix que de récupérer cette connaissance et, ce faisant, la force de stockage et la force de récupération sont améliorées. Si vous désirez approfondir ce sujet, voici un lien vers une mini-capsule vidéo que j'ai réalisée à cette fin :

Et pour les autres difficultés en mathématiques ?

Ah... effectivement, les difficultés en mathématiques ne se limitent pas aux faits multiplicatifs, n'est-ce pas ? Eh bien, il y a bien une autre mesure d'adaptation que j'aimerais vraiment, mais vraiment, devenir usuelle au Québec : des listes préapprouvées de vocabulaire disciplinaire.

En mathématiques, ce sont près de 600 mots que l'élève doit apprendre au cours de son primaire (Powell et al., 2021). Alors, imaginons un élève dont la difficulté est la consolidation des représentations phonologiques. Cet élève présente des difficultés à acquérir de nouveaux termes, et ce, particulièrement si ces termes ne sont utilisés qu'en scolaire et qu'une partie de l'année (ex. : parallèle). Dans le cas des difficultés d'accès lexical, l'élève a bien le mot quelque part en tête, mais il n'arrive pas à le récupérer. Quelle frustration !

De telles listes seraient fantastiques et répondraient réellement aux besoins spécifiques d'un tel élève. Classés en ordre alphabétique, les termes ne seraient pas regroupés par domaine ni associés à des exemples ou à leurs définitions. De telles listes diminueraient-elles le niveau de difficulté de la tâche ? À mon avis, elles ne serviraient à rien du tout si l'élève n'a pas étudié ou compris les concepts mathématiques en question. Par contre, en cas de "simple" difficulté d'accès lexical, l'élève pourrait survoler sa liste et repérer rapidement le terme recherché.

Encore une fois, au Québec, une telle mesure est fréquemment considérée être une modification... Faire inscrire cette mesure comme étant une adaptation dans un PI peut s'avérer un réel combat.

Au final, je salue l'évolution des mesures d'adaptation pour les difficultés d'orthographe lexicale ! Les dyslexiques et dysorthographiques de jadis n'ont pas eu la chance des élèves d'aujourd'hui.

J'ose espérer qu'une réflexion commune viendra pour mieux répondre aux besoins de l'élève présentant des difficultés mathématiques.

Références :

• Hansen, N., Jordan, N. C., Fernandez, E., Siegler, R. S., Fuchs, L., Gersten, R., & Micklos, D. (2015). General and math-specific predictors of sixth-graders’ knowledge of fractions. Cognitive Development, 35, 34–49.

• Hartman, J. R., Hart, S., Nelson, E. A., & Kirschner, P. A. (2023). Designing mathematics standards in agreement with science. International Electronic Journal of Mathematics Education, 18(3), em0739.

• Karpicke, J. D., 2012. Retrieval-based learning: Active retrieval promotes meaningful learning. Current Directions in Psychological Science, 21(3), 157-163.

• Powell, S. R., Bos, S. E., & Lin, X. (2021). The assessment of mathematics vocabulary in the elementary and middle school grades. Diversity Dimensions in Mathematics and Language Learning: Perspectives on Culture, Education and Multilingualism, edited by Annemarie Fritz, Erkan Gürsoy and Moritz Herzog, Berlin, Boston: De Gruyter, 2021, pp. 313-330. https://doi.org/10.1515/9783110661941-016

• Wortha, S. M., Klein, E., Lambert, K., Dackermann, T., & Moeller, K. (2023). The relevance of basic numerical skills for fraction processing: Evidence from cross-sectional data. PloS one, 18(1), e0281241.