Compréhension conceptuelle et fluence procédurale: en tandem !

Dans le milieu de l'éducation, l'idée que l'élève doit démontrer une compréhension conceptuelle suffisante (relativement à un concept particulier, tel que la division) avant d'être introduit aux procédures relatives à ce même concept (comme l'algorithme conventionnel de la division) perdure. Pourtant, aucune preuve empirique ne supporte une séquence d'enseignement particulière. La recherche supporte plutôt une relation BIDIRECTIONNELLE entre la compréhension conceptuelle et la fluence procédurale. Certes, on peut choisir de parfois mettre davantage l'accent sur l'une ou sur l'autre. Toutefois, la recherche ayant montré que les connaissances conceptuelles et procédurales se développent main dans la main, nous devons régulièrement établir explicitement des relations entre ces deux types de connaissances.

L'image ci-dessus illustre un enseignement dans lequel concepts et procédures sont explicitement liés. Dans cet exemple précis, les connaissances conceptuelles de la division sont introduites avant la procédure de division avec crochet (réf.: PDA en mathématiques). En effet, dans ce cas particulier, la procédure s'avère assez complexe et n'est donc introduite qu'au 3e cycle du primaire, alors que le concept de division est ciblé au cycle précédent. Les connaissances conceptuelles seront bien utiles pour appuyer l'apprentissage de cet algorithme.

Ainsi, dans cet exemple, j'ai d'abord réactivé les connaissances conceptuelles de l'élève : comment effectuer une division avec une représentation concrète (ex.: un matériel en base 10), puis semi-concrète (ex.: un dessin de la base 10). Rapidement toutefois (à notre 3e rencontre), j'ai introduit l'algorithme. Dès que l'élève avait terminé une distribution (par exemple celle des centaines), je réalisais un segment de l'algorithme qui correspondait à la représentation semi-concrète dessinée par mon élève. Ce faisant, j'expliquais verbalement en créant des liens explicites entre les deux représentations. Tout au long de l'activité, je la questionnais souvent. Petit à petit, elle eut davantage à faire dans l'algorithme, tout en continuant d'illustrer avec une représentation semi-concrète, à droite. Lorsqu'elle put réaliser tout cela sans support, nous avons délaissé la représentation semi-concrète, retirant ainsi un support qui ne devait être que temporaire. À cette étape, elle comprenait ce qu'elle faisait, pouvait répondre à diverses questions d'approfondissement et n'oubliait plus les étapes d'une mécanique non supportée par la compréhension conceptuelle. Les connaissances conceptuelles et procédurales commençaient à se consolider.

J'ai créé une séquence complète d'enseignement explicite de la division longue. J'ai aussi conçu quelques problèmes travaillés, merveilleux moyen de supporter l'élève en début d'apprentissage. Ce matériel est disponible sur mon site.

Bien que dans l'exemple illustré la compréhension conceptuelle semble effectivement précéder la fluence procédurale, rappelons que l'apprentissage se fait en tandem et donc, on cherchera à lier les deux types de connaissances lors de l'introduction de la procédure.

Il arrive parfois qu'une procédure plutôt simple soit accessible aux élèves en peu de temps, alors que le concept sous-jacent s'avère plus complexe à comprendre. Dans un tel cas, les connaissances procédurales pourraient être ciblées d'abord et, bien qu'on cherchera à faire des liens avec les concepts, ceux-ci pourraient être approfondis davantage une fois la procédure automatisée.

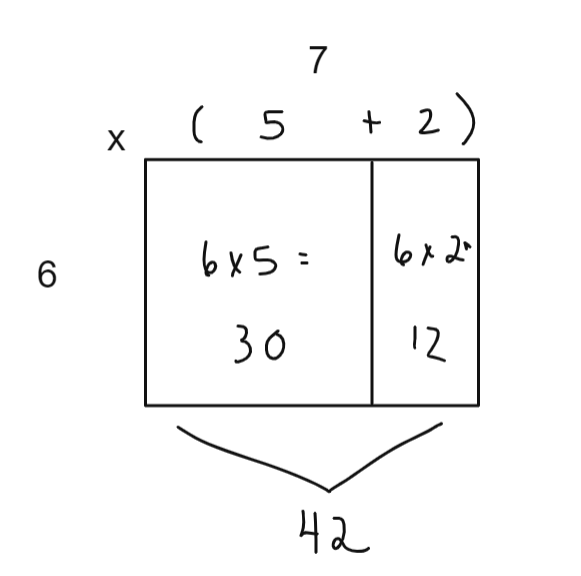
Prenons l'exemple de la distributivité. Traditionnellement, l'élève apprend une définition de cette propriété et s'exerce à reconnaître des exemples de celle-ci. Il aura également souvent à démontrer que cette propriété est vraie en validant que les deux côtés d'une équation (ex. : 3 x (40 + 5) = 3 x 40 + 3 x 5) sont effectivement équivalents. Puis, la procédure pourra devenir fluente si l'élève s'exerce suffisamment à calculer en se basant sur la propriété de la distributivité (ex. : 3 x (40 + 5) = ...). Ayant l'expérience de cette procédure réalisée maintes et maintes fois, l'élève pourra s'y référer pour approfondir ensuite ses connaissances conceptuelles de la distributivité. Notamment, des représentations semi-concrètes permettent d'illustrer qu'il s'agit d'une stratégie back-up courante lorsque le rappel d'un fait multiplicatif échoue (voir ci-dessous la stratégie appliquée au fait 6 x 7, le 7 étant ici décomposé en "5 + 2").

Les connaissances s'approfondissent également grâce aux discussions mathématiques. À quoi ça sert, cette propriété ? Dans la vraie vie, quand nous appuyons-nous sur elle pour effectuer un calcul mental ? Quelles sont les caractéristiques d'un calcul pour lequel la distributivité pourrait nous venir en aide pour réussir un calcul mental ? L'élève est-il alors à même de créer des exemples et des contre-exemples pour illustrer la distributivité ?

En résumé :

• Je retiens qu'une séquence d'enseignement C → P n'est pas supportée par la littérature. Concrètement, on pourrait avoir recours à des séquences variées : C → CP ; P → CP ; CP. En effet, il n'existe pas un ordre optimal d'enseignement (Rittle-Jonhson et al., 2015).

• Mettre d'abord une emphase plus importante sur les concepts (C) ou sur les procédures (P) pourrait varier en fonction de ce qui nous paraît une bonne porte d'entrée, un apprentissage à la portée des élèves. Celui-ci nous servira ensuite de levier.

• Je m'efforce de réfléchir aux moyens qui me permettront d'établir des relations explicites dans les connaissances conceptuelles set les connaissances procédurales.

Références :

Advocates for the Science of Math (2021). Common misconceptions: Conceptual and procedural understanding. Authors. https://www.thescienceofmath.com

Crooks, N. M., & Alibali, M. W. (2014). Defining and measuring conceptual knowledge in mathematics. Developmental Review, 34, 344-377.

Rittle-Johnson, B., & Alibali, M. W. (1999). Conceptual and procedural knowledge of mathematics: Does one lead to the other? The Journal of Educational Psychology, 91(1), 175-189.

Rittle-Johnson, B., Schneider, M., & Star, J. R. (2015). Not a one-way street: Bidirectional relations between procedural and conceptual knowledge of mathematics. Educational Psychology Review, 27, 587-597.

Schneider, M., Rittle-Johnson, R., & Star, J. R. (2011). Relations among conceptual knowledge, procedural knowledge, and procedural flexibility in two samples differing in prior knowledge. Developmental Psychology, 47(6), 1525-1538.