Au cours des vingt dernières années, deux modèles de services furent développés, en milieu scolaire, aux États-Unis : le modèle de Réponse à l’Intervention (RàI) et le Système de Soutien à Paliers Multiples (SSPM). Malgré leur implantation grandissante dans les pays anglo-saxons et au Québec, ces modèles de services sont encore peu connus dans les pays européens francophones (de Chambrier & Dierendonck, 2022). Je me permets donc de les dépeindre dans un premier temps. Nous verrons ensuite comment le dépistage universel en mathématiques s’inscrit dans de tels modèles.

Modèles de Réponse à l’Intervention (RàI) / Système de Soutien à Paliers Multiples (SSPM)

Les modèles de RàI / SSPM sont semblables, puisqu’ils sont tous deux conçus pour soutenir les apprentissages des élèves (dimension académique). Le SSPM offre toutefois un éclairage supplémentaire sur les dimensions socioémotionnelle et comportementale, visant ainsi le renforcement des comportements positifs (Burns et al., 2016). Ces modèles inclusifs ont été développés dans une optique préventive, pour favoriser la réussite de l’ensemble des élèves (Clarke et al., 2016). Ils permettraient en théorie une prise en charge plus précoce des élèves présentant des difficultés d’apprentissage qu’un modèle basé sur « l’attente de l’échec avant d’agir » (Desrochers & Guay, 2020).

Dans une telle approche, les élèves reçoivent des interventions basées sur des données probantes dans le cadre de trois paliers prévoyant une intervention de plus en plus intensive et spécifique. Ainsi, lorsqu’un élève montre une résistance à l’intervention au 1er palier, lequel consiste en un enseignement de haute qualité, offert en classe à l’ensemble des élèves, il est orienté au palier 2, où le dosage est augmenté. La persistance des difficultés n’est pas laissée au jugement de l’enseignant ni aux résultats des évaluations sommatives. Elle se doit d’être objectivée par l’utilisation de brèves mesures critériées dont l’utilisation régulière permet la collecte de données objectives et le suivi des progrès. Ce suivi assure le repérage des élèves dont la progression se révèle insuffisante au palier 1, voire au palier 2. Le cas échéant, le palier 3 prévoit l’intervention la plus intensive et ciblée, généralement offerte par un intervenant spécialiste tel que l’orthophoniste ou l’orthopédagogue, au Québec.

Ce type d’approche nécessite la collaboration de plusieurs intervenants : directions, enseignants et spécialistes en intervention et en analyse de données (comme les orthophonistes, les orthopédagogues ou les psychologues).

Dépistage universel en mathématiques dans le cadre des modèles de RàI / SSPM

Avant toute chose, il importe de préciser le but d’un dépistage universel en mathématiques : identifier le plus précisément possible les élèves à risque d’échouer ultérieurement à une mesure générale de compétence mathématique. Dans un contexte réel scolaire, un tel dépistage cherche à prédire quels élèves seront en échec en mathématiques (par exemple, au terme de l’année scolaire) si on ne leur offre pas un support supplémentaire, celui-ci étant nécessaire à leur réussite.

Un tel dépistage ne cherche pas à identifier une liste de compétences fragiles qui feraient de bons objectifs d’intervention. C’est une démarche pour sélectionner les élèves, pas les objectifs.

Dans l’approche des modèles de RàI / SSPM, le dépistage universel s’adresse à tous les élèves ou presque. Si les difficultés mathématiques de certains ont déjà été avérées, notamment dans le cadre d’une évaluation approfondie en cognition mathématique, inutile que ces élèves prennent part au dépistage universel (après tout, on les a déjà identifiés comme des élèves ayant assurément besoin de support supplémentaire). On proposera donc un dépistage universel à la presque totalité des élèves dans un parcours scolaire régulier, et ce, chaque année. Des chercheurs recommandent d’ailleurs trois passations annuelles, soit à l’automne, à l’hiver et au printemps (Lembke et Stecker, 2007; VanDerHeyden et Muyskens, 2023).

Le dépistage universel requiert évidemment une mesure simple sur le plan de la passation, de la cotation et de l’analyse, mais elle se doit surtout d’être brève. En effet, si la durée n’est pas un enjeu dans le contexte d’un dépistage d’un élève unique en bureau privé, il en est autrement lorsqu’une passation est planifiée pour un grand groupe d’enfants. Dans ce contexte, une mesure de passation individuelle devrait être complétée en 5 à 10 minutes (Seethaler et al., 2016; Purpura et al., 2015). Quoi qu’il en soit, une passation individuelle, même brève, exige un temps considérable. Pour une classe de 22 élèves, on comptera par exemple 110 minutes de passation totale pour une mesure complétée en 5 minutes par enfant. À cela s’ajoute bien entendu le temps alloué aux transitions entre les élèves ainsi que la cotation et l’analyse ultérieures.

Ainsi, la modalité de passation est un autre facteur à considérer sérieusement, car une passation collective offre évidemment une économie de temps substantielle.  Or, une telle passation exige que les élèves répondent par écrit. Cette modalité de réponse n’est potentiellement pas adaptée en maternelle, voire même au début de la 1re année du primaire, alors que les réponses orales ou par pointage permettent de mieux apprécier les habiletés individuelles. Quoi qu’il en soit, la passation collective sera certes privilégiée dès que possible (Clarke et Shinn, 2004).

Si la durée et la modalité de passation sont des considérations pratiques non négligeables, la mesure sélectionnée doit aussi satisfaire d’autres critères cruciaux. En effet, le dépistage universel sert un objectif de grande importance : identifier le plus précisément possible les élèves à risque de difficultés mathématiques. On souhaite évidemment aussi minimiser les faux positifs (c’est-à-dire le classement dans la catégorie « à risque » d’un jeune qui réussira pourtant ultérieurement à la mesure générale de compétence mathématique), en raison des coûts (en ressources humaines) associés au support supplémentaire offert à ces élèves… qui n’en avaient finalement pas besoin. Dans un monde idéal, l’outil utilisé présenterait donc une bonne validité prédictive (il serait corrélé à la mesure ultérieure d’un test général de compétence mathématique), une bonne sensibilité (il permettrait d’identifier précisément tous les élèves « à risque ») et serait également spécifique (c’est-à-dire qu’il identifierait également de manière précise tous les élèves « non à risque »). Or, il s’avère que l’élaboration d’une telle mesure unique semble utopique.

Un dépistage en deux phases, nommé gated screening ou two-phase approach dans la littérature américaine, semble toutefois prometteur (Van Norman et al., 2019; VanDerHeyden et al., 2019; Seethaler et al., 2016) pour réaliser ce tour de force. Une telle approche consiste en l’utilisation de deux mesures distinctes, dont la combinaison aurait un meilleur pouvoir discriminant, conduisant à une meilleure classification des élèves dans leurs catégories respectives : « à risque » ou « non à risque » de présenter des difficultés d’apprentissage en mathématiques. Bien qu’une telle procédure exige davantage de temps, elle s’avère en fin de compte moins coûteuse qu’une suridentification d’élèves en difficulté, orientés sans vraie nécessité vers une intervention au palier 2 d’un modèle de RàI / SSPM, ce qu’une mesure sensible, mais peu spécifique, entraîne nécessairement.

Dépistage universel : phase 1

La première mesure de dépistage, dans le cadre d’une approche en deux phases, se veut simple d’utilisation, courte et surtout très sensible, réduisant au maximum les faux négatifs. On voudra avant tout s’assurer qu’aucun élève à risque ne passe entre les mailles de ce premier filet. Le développement d’une telle mesure occasionne un sacrifice. En maximisant la sensibilité d’un outil, on en réduit généralement la spécificité. Autrement dit, ce type d’outil mène parfois à l’identification d’une très grande quantité d’élèves à risque, incluant nécessairement des faux positifs (Purpura et al., 2015).

Par exemple, dans le cadre d’une étude menée par VanDerHeyden et al. (2019), un dépistage universel a mené à l’identification de 81% des élèves de maternelle comme étant à risque. Ce premier dépistage aura permis l’identification des élèves qui, assurément, ne présentent pas de difficulté en mathématiques (par exemple, 19 % des élèves de maternelle testés dans cette étude présentent manifestement de bonnes compétences). Cependant, les élèves identifiés « à risque » n’allaient certainement pas tous échouer, en fin d’année, à l’épreuve de compétence globale en mathématiques… Il va sans dire qu’on ne pourrait d’ailleurs considérer offrir des services au palier 2 à une si grande proportion des élèves.

D’autre part, de tels résultats étonnent, car ils s’éloignent manifestement de la distribution normale théorique de 20 % d’élèves en difficulté pour 80 % d’élèves présentant une progression satisfaisante au palier 1 (Batsche et al., 2005). Or, selon VanDerHeyden et Muyskens (2023), la majorité des outils de dépistage en mathématiques sont trop faciles. Ainsi, ils manquent de sensibilité, et ce, afin de forcer une distribution normale des résultats. Pourtant, la constitution des classes varie énormément, notamment en fonction de la vulnérabilité socioéconomique de certains milieux, et donc, le taux de risque de base d’un groupe (c’est-à-dire le pourcentage des élèves à risque dans un groupe particulier) est parfois bien plus élevé que ce 20 % théorique. Deux constatations s’ensuivent. D’une part, en présence d’un haut taux de risque de base, c’est-à-dire au sein d’un groupe dont le pourcentage d’élèves en difficulté surpasse nettement 20 %, tous les élèves identifiés à risque ne peuvent accéder au palier 2 du modèle de RàI / SSPM, afin d’y recevoir une rééducation à grand dosage. En effet, au palier 2, un élève reçoit généralement une intervention en groupe de 4 à 6 élèves, et ce, à raison de 3 à 5 séances de 30 minutes pendant 8 à 16 semaines (Austin et al., 2017). Ce type de services engendre des coûts non négligeables et donc, les élèves sélectionnées pour le palier 2 doivent être en quantité limitée.

D’autre part, lorsqu’un dépistage révèle un haut pourcentage d’élèves à risque, force est de constater que ces élèves ne progressent pas suffisamment avec l’enseignement qui leur est offert au palier 1. Ils nécessitent un enseignement basé sur les données probantes et potentiellement aussi un dosage accru. Le temps de classe ne pouvant être augmenté, il s’agira de cibler les savoirs fondamentaux et d’assurer plus de temps sur ceux-ci, dans le cadre d’un enseignement explicite.

Ainsi, en présence d’une proportion importante d’élèves à risque dans une classe, le palier 1.5 a été récemment reconnu essentiel par certains chercheurs (voir figure 1). Ce palier consiste en la mise en place d’une intervention rigoureuse, offerte par l’enseignant au groupe entier, dans les heures régulières de classe. Des données relatives au suivi des progrès de chaque élève sont alors recueillies minimalement une fois par semaine et servent à identifier de manière plus spécifique, après quelques semaines, les élèves nécessitant une intervention supplémentaire au palier 2. Une telle intervention en groupe-classe constitue la mesure de deuxième phase recommandée par certains chercheurs lorsque plus de 50 % des élèves d’un groupe sont classés « à risque » au cours de la phase 1 (VanDerHeyden, 2013; VanDerHeyden et Muyskens, 2023; Kovaleski et al., 2022).

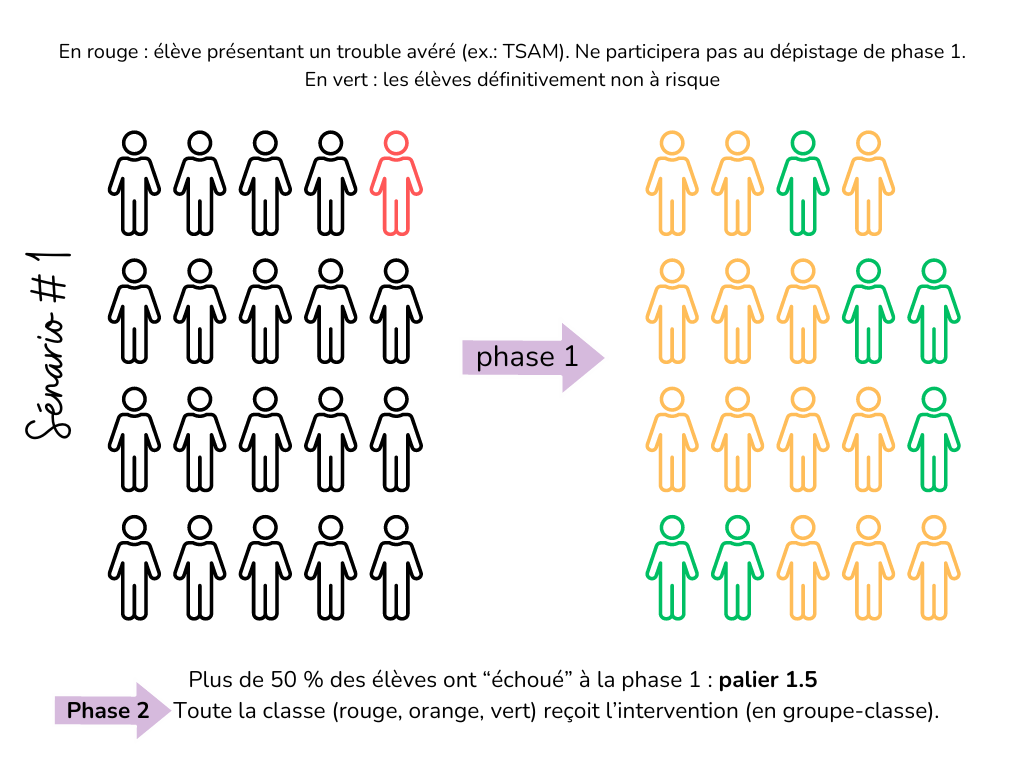
Figure 1. Exemple théorique illustrant un groupe à haut taux de risque de base (Plus de 50 % des élèves sont sous le seuil de risque d’une mesure sensible utilisée en phase 1. Ces élèves sont identifiés en jaune.)

L’étude de VanDerHeyden et al. (2019) est particulièrement intéressante pour nous, francophones. En effet, bien qu’elle soit américaine, les mesures employées s’avèrent peu ou pas sensibles à la langue. À titre indicatif, à l’automne de la 3e année du primaire, trois mesures étaient employées :

1. Additions et soustractions entremêlées (sommes de 20 et moins ; premier terme de la soustraction de 20 et moins)

2. Additions de nombres à 3 chiffres avec et sans échanges ;

3. Soustractions de nombres à 3 chiffres avec et sans échanges.

Ces mesures, nommées « mesures basées sur le curriculum » (CBM, soit Curriculum Based Measurements) ne sont pas corrigées uniquement en termes de bonnes réponses. En effet, les scores des élèves doivent refléter à la fois précision et vitesse. Ils permettent ainsi d’identifier le niveau de performance de chaque élève, tels que définis en 1977 par Deno et Mirkin, soit : le niveau de frustration (caractérisé par une faible précision et une faible vitesse), suivi du niveau d’apprentissage (caractérisé par une bonne précision, mais une faible vitesse) et ultimement du niveau de maîtrise (caractérisé par une bonne fluence, soit une bonne précision et une bonne vitesse). Si vous désirez approfondir cette notion, je vous réfère à une fiche informative que j’ai rédigée sur le sujet :

Dans l’exemple ci-dessous (figure 2), la mesure utilisée en phase 1 en était une de calcul simple. Les élèves devaient résoudre des additions dont les termes étaient de 10 ou moins (ex. : 4 + 8 ) et des soustractions dans le premier terme était de 20 ou moins, le deuxième terme étant un nombre à un seul chiffre et la différence étant un nombre à un chiffre également (ex. : 13 – 6), et ce, le plus rapidement possible. Les deux élèves classés « non à risque » (bandes turquoise) sont les seuls ayant dépassé le seuil de la zone d’apprentissage associé à leur niveau scolaire, soit 21 chiffres corrects par deux minutes. Autrement dit, en deux minutes, ils ont écrit plus de 21 chiffres corrects sur leur copie, en réponse aux calculs présentés dans la mesure.

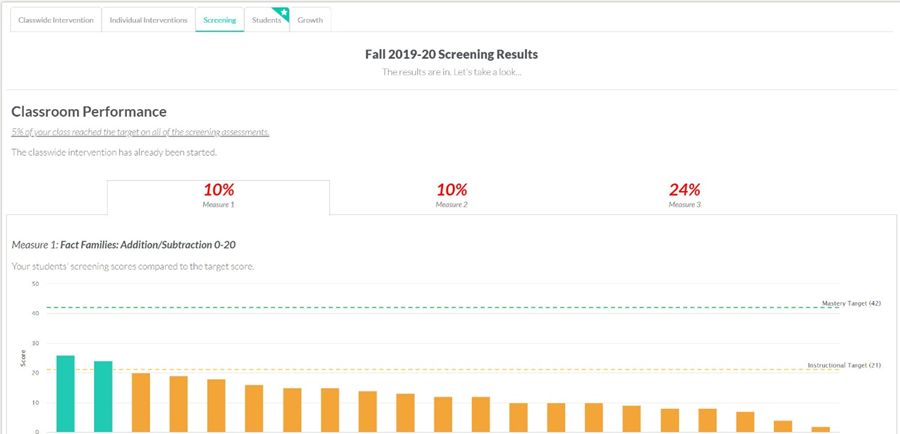
Figure 2. Exemple réel illustrant un groupe à haut taux de risque de base. Plus de 50 % des élèves sont sous le seuil de risque, soit la cible d’apprentissage désignée par la ligne pointillée orangée (figure reproduite avec permission, tirée du guide Supporting Math MTSS Through SpringMath, VanDerHeyden et Muyskens, 2023; graphique produit grâce à SpringMath, www.springmath.org).

Dépistage universel : phase 2

Groupes présentant un haut taux de risque de base

La phase 2 du dépistage universel peut prendre plusieurs formes. Comme nous venons de l’aborder, l’intervention en groupe-classe (palier 1.5) serait l’avenue à privilégier quand plus de la moitié des élèves d’un groupe performent sous le critère minimal de la mesure utilisée en phase 1 (voir figures 1 et 2).

Dans un tel scénario, tous les élèves de la classe prennent part à l’intervention : les meilleurs comme les élèves à risque et les élèves présentant un trouble des apprentissages en mathématiques. C’est ainsi qu’après quelques semaines, la progression des élèves, mesurée régulièrement grâce à de courtes mesures critériées, permet le repérage de ceux dont l’évolution s’avère insuffisante (VanDerHeyden et al., 2019; VanDerHeyden et Muyskens, 2023) (voir figure 3).

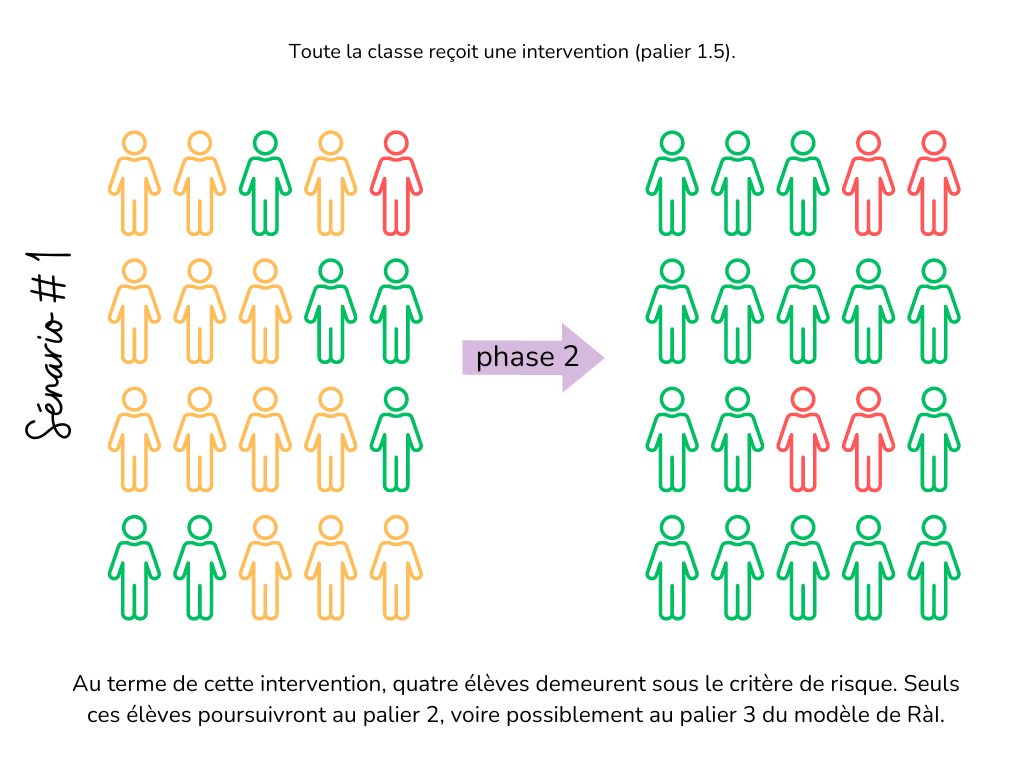
Figure 3. Exemple théorique illustrant un groupe à haut taux de risque de base (Plus de 50 % des élèves sont sous le seuil de risque d’une mesure sensible utilisée en phase 1. Ces élèves sont identifiés en jaune.) Suite à l’intervention offerte au palier 1.5 (qui représente la deuxième mesure du gated-screening), seuls quatre élèves sont confirmés « à risque ».

Mais comment trancher ? Dans ses travaux, VanDerHeyden fixe le seuil de risque de l’intervention au palier 1.5 comme suit : lorsque le score médian du groupe atteint le seuil de maîtrise (pour une habileté ciblée dans l’intervention en groupe-classe), tout élève se situant encore au niveau de la frustration est confirmé à risque (voir figure 4).

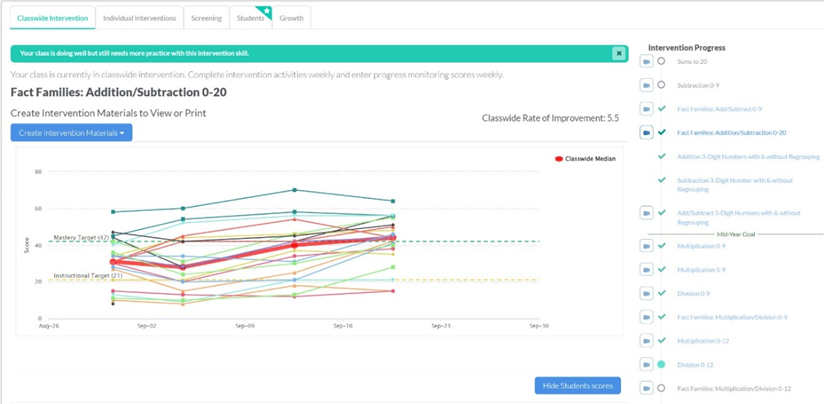
Figure 4. À la suite de 4 semaines d’intervention en classe, la médiane du groupe (en rouge, en gras) a atteint le seuil de maîtrise (ligne turquoise pointillée), ce qui marque la fin de l’intervention ciblant les additions et soustractions 0-20. Seulement quatre élèves se situent alors toujours sous le seuil de risque, identifié par la ligne pointillée orangée (figure reproduite avec permission, tirée du guide Supporting Math MTSS Through SpringMath, VanDerHeyden et Muyskens, 2023; graphique produit grâce à SpringMath, www.springmath.org).

Si une intervention en groupe-classe semble simplement être la solution logique pour pallier une problématique qui touche la majorité d’un groupe, il s’avère que ce type d’intervention a aussi fait ses preuves comme moyen permettant une classification plus précise des élèves parmi les catégories « à risque » et « non à risque » (VanDerHeyden, 2013). Il s’agit d’une excellente « phase 2 » dans le cadre d’un gated-sreening. En effet, les données relatives au suivi des progrès s’intéressent directement à la résistance à l’intervention. La figure 5 illustre bien comment l’usage unique de la mesure de dépistage en phase 1 n’aurait pas tout à fait conduit à l’identification des mêmes élèves si on avait décidé d’offrir un support au palier 2 au plus faible 20 % des élèves. La sélection de ce plus faible 20 % (c’est-à-dire les 4 élèves à l’extrême droite du graphique en figure 5) aurait inclus deux faux positifs, mais pire encore, deux des quatre élèves vraiment vulnérables (ceux identifiés par les flèches bleues) auraient été exclus et n’auraient donc pas été orientés au palier 2.

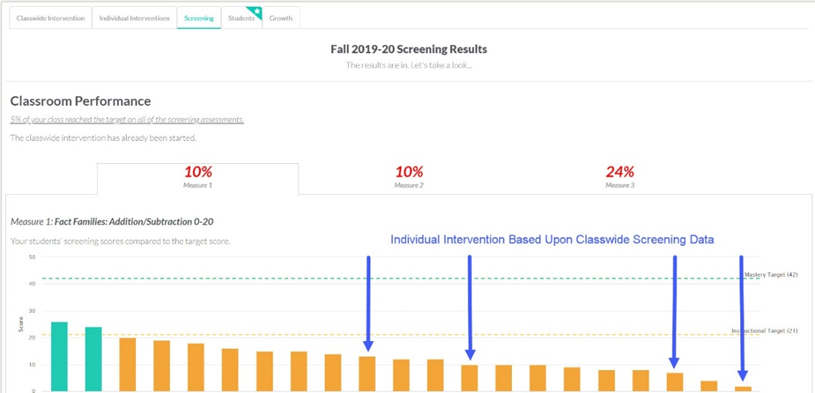
Figure 5. Les élèves qui se situent toujours sous le seuil de risque au terme de l’intervention sont ici identifiés par des flèches bleues, dans le graphique de la mesure initiale en phase 1. La phase 2 a donc réduit de 24 à 4 la quantité d’élèves nécessitant une intervention au palier 2 du modèle de RàI (figure reproduite avec permission, tirée du guide Supporting Math MTSS Through SpringMath, VanDerHeyden et Muyskens, 2023; graphique produit grâce à SpringMath, www.springmath.org).

Groupes présentant un taux de risque de base plus réduit

Lorsque le taux de risque de base de la classe s’avère plus réduit (moins de 50 % des élèves étant identifiés à risque dans la phase 1), la phase 2 du dépistage en deux phases n’est proposée qu’aux élèves repérés par la première mesure (voir figure 6).

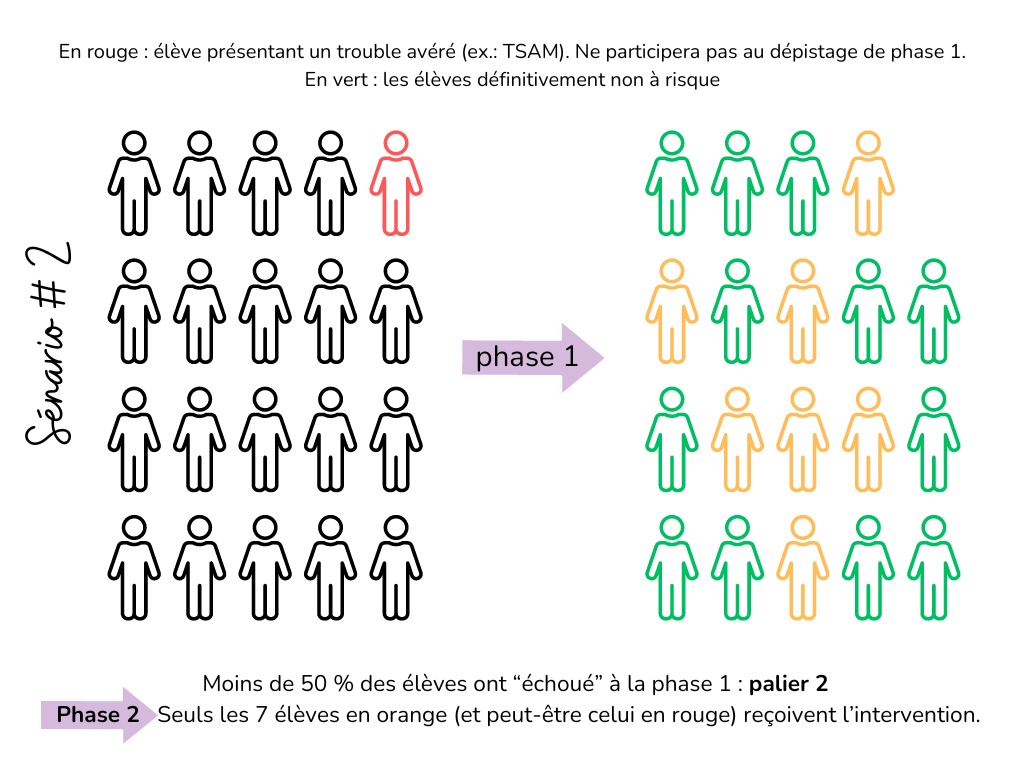
Figure 6. Exemple théorique illustrant un groupe avec taux de risque de base plus réduit (moins de 50 % des élèves sont sous le seuil de risque d’une mesure sensible utilisée en phase 1. Ces élèves sont identifiés en jaune.)

En effet, l’intervention en groupe-classe ne serait pas justifiée, car la majorité des élèves n’en ont pas besoin. Les mêmes mesures basées sur le curriculum (CBM) pourraient néanmoins être utilisées (Lembke & Stecker, 2007). Combinée à une intervention non individualisée (le sous-groupe entier reçoit la même intervention), la prise de données hebdomadaire permet de suivre le progrès des élèves ciblés. Le critère de risque, cette fois, ne peut évidemment pas être établi en référence à la médiane du sous-groupe, puisque l’ensemble est vulnérable.  Il s’avère donc essentiel de fixer un objectif correspondant à l’atteinte de la zone de maîtrise d’une habileté spécifique, ainsi qu’un nombre de séances ou de semaines pour y parvenir. Lorsque la progression d’un élève se révèle sous les attentes, le risque est confirmé et l’intervention devra être adaptée (sélection d’objectifs) et intensifiée davantage (au palier 2, voire au palier 3), dans le cadre d’un modèle de RàI / SSPM (voir figure 7).

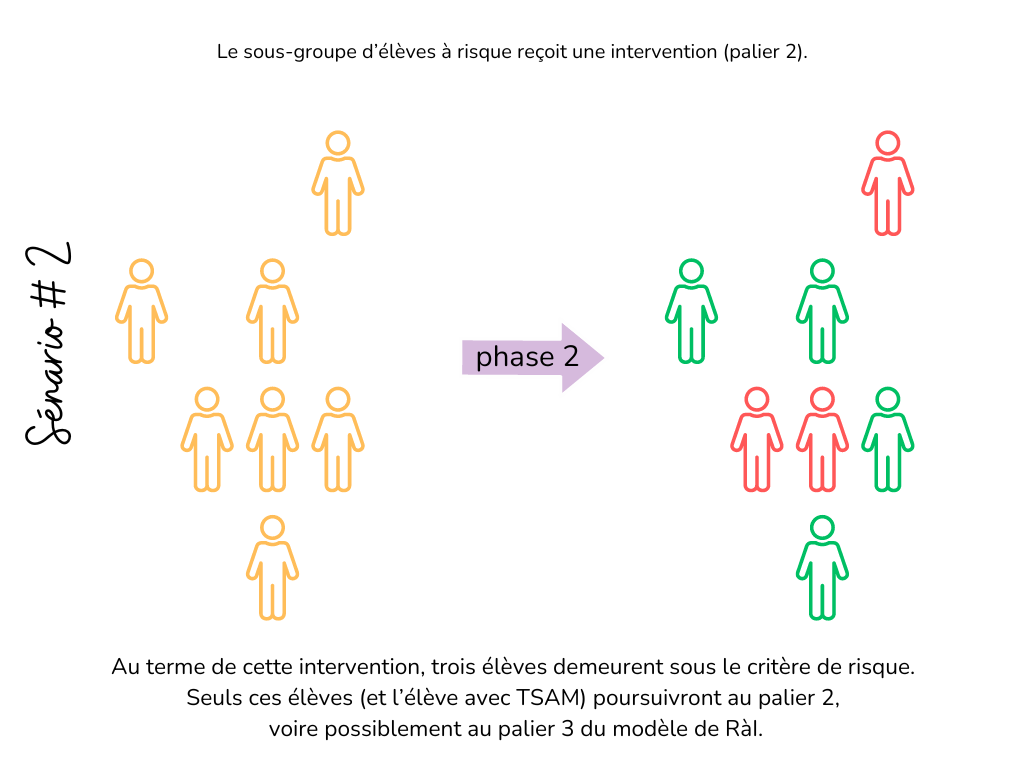
Figure 7. Exemple théorique illustrant un groupe à taux de risque de base réduit (Moins de 50 % des élèves sont sous le seuil de risque d’une mesure sensible utilisée en phase 1. Ces élèves sont identifiés en jaune.) Suite à l’intervention offerte au palier 2 (qui représente la deuxième mesure du gated-screening), seuls trois élèves sont confirmés « à risque ».

Quoi qu’il en soit, d’autres types de mesures (que les CBM) ont également fait leurs preuves pour conclure une approche de dépistage en deux phases. En effet, une évaluation dynamique (Fuchs et al., 2008; Seethaler et al., 2011; Fuchs et al., 2012) ou une évaluation statique sont aussi proposées dans la littérature. Ces mesures plus approfondies doivent prioriser la spécificité sur la sensibilité, en accord avec les principes d’une approche en deux phases, pour éviter d’offrir une intervention coûteuse aux élèves qui, finalement, n’en ont pas vraiment besoin (c’est-à-dire aux faux positifs).

Voici un tableau résumant les éléments essentiels couverts par ce billet, relativement au dépistage universel en mathématiques dans le cadre d’un modèle de RàI / SSPM :

Tableau 1. Résumé relatif au dépistage universel en mathématiques dans le cadre d’un modèle de RàI / SSPM

Et ensuite ?

J’ai écrit, un peu plus haut, que le but du dépistage universel, c’est d’identifier des élèves, pas des objectifs. D’accord. Mais alors, quand on les a identifiés, ces élèves à risque (ceux en rouge dans les figures 3 et 7), on fait quoi ? On s’entendra tous, je l’espère, sur le fait que d’identifier les élèves à risque juste pour les identifier serait un drame.

Eh bien, ça prend certainement un autre type d’outil : un dépistage qu’on pourrait qualifier de deuxième intention. Celui-ci pourra être un peu plus long, mais surtout, il ciblera un éventail de compétences mathématiques considérées en recherche comme fondamentales à la réussite de l’élève (ex. : la fluence arithmétique, la résolution de problèmes arithmétiques, la compréhension du vocabulaire mathématique, le jugement proportionnel sur droite numérique, etc.). L’objectif est bien, cette fois-ci, de sélectionner des objectifs d’intervention, en situant l’élève en référence à des données développementales.

De nouveau, en français, peu d’outils ont été développés pour cet usage. Afin de cibler ses objectifs, le professionnel pourrait créer ses propres épreuves critériées et se référer aux données développementales extraites de la littérature scientifique. J’ai moi-même développé un protocole de dépistage à cet effet, pour les jeunes de 3 à 8 ans. Je vous invite à en apprendre davantage sur le PDCM 3-8, si cet outil peut répondre à vos besoins.

D’aute part, concernant spécifiquement le vocabulaire mathématique, deux outils initialement développés par des chercheuses américaines ont été dernièrement traduits et adaptés pour le Québec, avec l’accord de l’autrice principale, Sarah R. Powell. Ces mesures sont conçues soit pour le 2e cycle du primaire, soit pour le 3e cycle du primaire. En téléchargeant ces produits gratuits, vous aurez notamment accès à un guide explicatif complet.

Conclusion

Le dépistage universel en mathématiques n’est certes pas une mince affaire à tenter d’implanter dans notre réalité québécoise. Les articles en référence étant en grande majorité américains, les chercheurs y proposent des outils anglophones... mais les mesures basées sur le curriculum ne sont souvent pas sensibles à la langue et les données proposées par Deno et Mirkin ne varient pas en fonction de la mesure. Par exemple, pour un élève de la 3e à la 6e année primaire, la zone d’apprentissage correspond à une fluence arithmétique de 20 à 39 chiffres corrects par minute (DCPM). Un score inférieur à 20 DCPM serait donc sous le seuil de risque, en référence aux travaux d’Amanda VanDerHeyden. Toujours faut-il néanmoins savoir choisir des mesures offrant des calculs adaptés au niveau scolaire des élèves.

Mon souhait est que cette lecture vous ait renseigné sur l’état des lieux chez nos voisins du sud. L’ampleur de la tâche derrière l’implantation d’un dépistage universel est bien supérieure à ce que je m’imaginais moi-même, avant de me plonger dans ces articles. Un dépistage universel réalisé avec un outil questionnable pourrait avoir de fâcheuses conséquences. D’un autre côté, choisir de ne pas réaliser de dépistage universel, c’est attendre l’échec et mettre une croix sur l’intervention préventive. Il s’agit sans aucun doute d’une problématique à laquelle nous devrons nous attaquer…

Bonne réflexion !

Références

Austin, C. R., Vaughn, S., & McClelland, A. M. (2017). Intensive Reading Interventions for Inadequate Responders in Grades K–3: A Synthesis. Learning Disability Quarterly, 40(4), 191–210. https://www.jstor.org/stable/26742876

Batsche, G., Elliott, J., Graden, J. L., Grimes, J., Kovaleski, J. F., Prasse, D., Schrag, J., & Tilly, W. D. (2005). Response to Intervention: Policy Considerations and Implementation. Alexandria, VA: National Association of State Directors of Special Education, Inc.

Burns, Matthew & Jimerson, Shane & Vanderheyden, Amanda & Deno, Stanley. (2016). Toward a Unified Response-to-Intervention Model: Multi-Tiered Systems of Support. 10.1007/978-1-4899-7568-3_41.

Clarke, B., Doabler, C. T., Smolkowski, K., Baker, S. K., Fien, H., & Strand Cary, M. (2016). Examining the efficacy of a tier 2 kindergarten mathematics intervention. Journal of Learning Disabilities, 49, 152– 165. doi: 10.1177/0022219414538514

Clarke, Ben & Shinn, Mark. (2004). A Preliminary Investigation Into the Identification and Development of Early Mathematics Curriculum-Based Measurement. School psychology review. 33. 234-248. 10.1080/02796015.2004.12086245.

De Chambrier, Anne-Françoise & Dierendonck, Christophe. (2022). Vers l’implémentation du modèle de Réponse à l’Intervention dans les systèmes éducatifs d’Europe francophone ?. L’Année psychologique. Vol. 122. 301-337. 10.3917/anpsy1.222.0301.

Deno, S. L. (1985). Curriculum-Based Measurement: The Emerging Alternative. Exceptional Children, 52(3), 219-232.

Desrochers, A. & Guay, M.-H. (2020). L’évolution de la réponse à l’intervention : d’un modèle d’identification des élèves en difficulté à un système de soutien à paliers multiples. Enfance en difficulté, 7, 5–25. https://doi.org/10.7202/1070381ar

Fuchs, L. S., Compton, D. L., Fuchs, D., Hollenbeck, K. N., Craddock, C. F. et Hamlett, C. L. (2008). Dynamic Assessment of Algebraic Learning in Predicting Third Graders' Development of Mathematical Problem Solving. Journal of educational psychology, 100(4), 829–850.

Fuchs, D., Fuchs, L. S. et Compton, D. L. (2012). Smart RTI: A Next-Generation Approach to Multilevel Prevention. Exceptional children, 78(3), 263–279.

Kovaleski, J., VanDerHeyden, A. M., Runge, T., Zirkel, P. et Shapiro, E. (2022). The RtI Approach to Evaluating Learning Disabilities, 2nd Edition. NY: Guilford.

Lembke, E. et Stecker, P. (2007). Curriculum-based measurement in mathematics: An evidence-based formative assessment procedure. Portsmouth, NH:RMC Research Corporation, Center on Instruction.

Purpura, D. J., Reid, E. E., Eiland, M. D. et Baroody, A. J. (2015). Using a brief preschool early numeracy skills screener to identify young children with mathematics difficulties. School Psychology Review, 44(1), 41-59.

Seethaler, P. M., Fuchs, L. S., Fuchs, D., & Compton, D. L. (2012). Predicting First Graders' Development of Calculation versus Word-Problem Performance: The Role of Dynamic Assessment. Journal of educational psychology, 104(1), 224–234.

Seethaler, P. M., Fuchs, L. S., Fuchs, D., & Compton, D. L. (2016). Does the Value of Dynamic Assessment in Predicting End-of-First-Grade Mathematics Performance Differ as a Function of English Language Proficiency? The Elementary School Journal, 117(2), 171–191.

VanDerHeyden, A. M. (2013). Universal screening may not be for everyone: Using a threshold model as a smarter way to determine risk. School Psychology Review, 42(4), 402-414.

VanDerHeyden, A. M., Broussard, C. et Burns, M. K. (2019). Classification Agreement for Gated Screening in Mathematics: Subskill Mastery Measurement and Classwide Intervention. Assessment for Effective Intervention, 46(4), 270-280.

VanDerHeyden, A. M. et Muyskens, P. (2023). Supporting Math MTSS Through SpringMath : Your guide to driving math mastery, SpringMath by Sourcewell, https://www.springmath.org/sites/default/files/2024-01/SpringMath_Technical_Manual_Users_Guide_0124_bk_Final_Web_2.pdf

Van Norman, E. R., Nelson, P. M., Klingbeil, D. A., Cormier, D. C. et Lekwa,  A. J. (2019). Gated Screening Frameworks for Academic Concerns: the Influence of Redundant Information on Diagnostic Accuracy Outcomes. Contemp School Psychol, 23, 152-162.